ML and DL Collaborative Filters
by Alberto Gutierrez, November 8, 2019
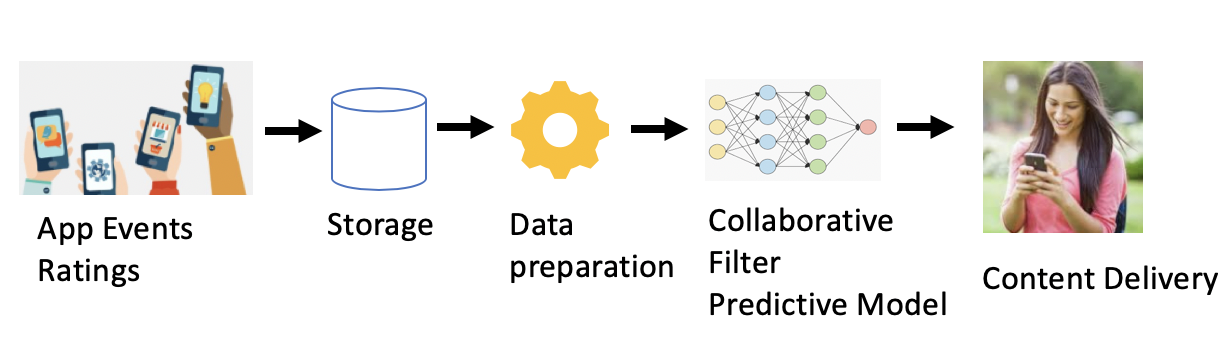
Introduction
Our objective in this exercise is to understand, through evaluation and coding, how deep-learning recommender models can improve on the performance of conventional machine learning collaborative filter recommender models. However, before diving into the coding, it is helpful to set the context by first identifying business applications where recommendation algorithms are applied. Next, we discuss a few common recommender algorithms to understand where the collaborative filter fits within the context of these solutions. Following this introduction, we evaluate the performance of a conventional machine learning recommender model, a matrix factorization collaborative filter. Then we evaluate several deep-learning models that offer progressively better predictive capability. From this evaluation, we observe several features of the deep-learning models that are responsible for their performance improvement over the basic Matrix Factorization approach.
Business Applications
In the last several years, recommendation systems, along with other predictive algorithms, have become an essential staple in several business applications. From the technical point of view, we are motivated to provide better algorithms, and this, in turn, leads to better business results. For example, several business applications where recommender technology is applied are enumerated below.
- e-commerce - shopping, retail, groceries
- Movie recommendation
- Mobile app content delivery
- Customer engagement, customer journey analytics
- Dating (matchmaking)
- Advertising - offers, up-sell, cross-sell offers
- Music recommendation
The business goal is to maximize the chances that the consumer will click, like, buy, or open the recommended content. Ultimately, the recommendation system contributes to improved customer engagement, revenue, and total lifetime value (TLV). For example, as a rule of thumb, engaged customers represent 23% premium in the share of wallet compared to an average customer.
Collaborative Filter Algorithms
In the context of business applications there is no one size fits all model. Therefore, to get some appreciation for where the collaborative filter fits with other prominent recommendation algorithm types, it is useful to identify common recommender algorithms chosen during a simplified e-commerce customer journey. The type of model chosen is largely dependent on the use case so as to bring better benefit to the consumer.
When first entering an e-commerce site, a collaborative filter model is often employed to give a recommendation based on an optimized prediction of what the user will like based on the combination of other user’s choices. This classic approach is known as Latent Factors, where the matrix factorization approach became popular as a result of the Netflix competition. As the consumer proceeds on their journey, and as they interact with content, then this is an opportunity to present recommendations based on item-item preferences, that is, other items “like the one you are looking at.” On the other hand, as the consumer proceeds on the journey, there may be opportunities to help them decide with user-item similarity. In this case, items are recommended based on other users that are similar to the active user. For example, user-item and item-item based filtering is an overview of recommended items based on similar users or items that are similar to other items, respectively.
Software
We make use of the Fastai Library library that sits above Pytorch to evaluate the models. Much credit goes to Fastai for motivating this exercise based on a class discussion and example Fastai collaborative filter github. Additionally, a complete Jupyter notebook for the code discussed in the examples below is available in Github.
Dataset
For this exercise we employ the Movielens 100K data set.
ratings.head()
userId movieId rating timestamp
1 1 4.0 964982703
1 3 4.0 964981247
1 6 4.0 964982224
1 47 5.0 964983815
1 50 5.0 964982931
Benchmarks
We want to ensure that the performance of the models is competitive to best in class performance, so we compare our model performance to world-class benchmarks. For the MovieLens 100K dataset (as used in this article) the popular Librec system reports best in class performance of RMSE = 0.91, which is helpful to gauge the effectiveness of the models evaluated here.
Matrix Factorization Collaborative Filter
We begin by analyzing the performance of the matrix factorization latent factors model.
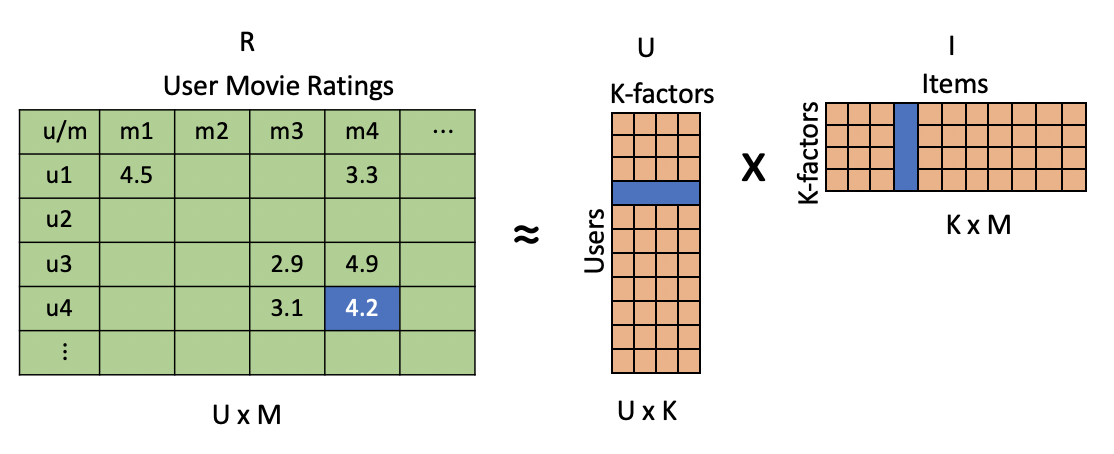
Latent Factors, matrix factorization with SGD
With reference to the figure above, the matrix factorization method forms an approximation to the sparse ratings matrix, R. For example, in a simplistic way, we can think of the latent factors as genres of dimension K, such as Western, SciFi, and Drama, etc. User Factors correspond to the extent that a user likes the genre. Item Factors correspond to the extent that a movie corresponds to the genre. An approximation to the ratings matrix is formed by the multiplication of the User Factor and Item Factor matrices, where the number of latent factors, K, is a design parameter (i.e., hyperparameter). The content of the user factor matrices is found with algorithms such as ALS (Alternating Least Squares) and are readily available via open-source software frameworks such as with the Spark, MLLiB - Collaborative Filter with ALS and Latent Factors.
Matrix Factorization Collaborative Filter Model
Below is the collaborative filter matrix factorization model. The class utilizes the PyTorch nn.Module, and makes use of nn.Embeddings to hold the user and items matrices. The forward method receives categorical variables (“cats”) and continuous variables (“conts”) though we do not use the continuous variables. Since the Fastai library provide both types of variables, we keep the continuous variables available for potential use at a later time. The forward function returns the matrix multiplication of the two matrices.
class MFCF(nn.Module):
def __init__(self, n_users, n_items):
super().__init__()
self.u = nn.Embedding(n_users, n_factors)
self.m = nn.Embedding(n_items, n_factors)
self.u.weight.data.uniform_(0,0.05)
self.m.weight.data.uniform_(0,0.05)
def forward(self, cats, conts):
users,items = cats[:,0],cats[:,1]
u,m = self.u(users),self.m(items)
return (u*m).sum(1).view(-1, 1)
Next, we create unique indexes for movies and ratings and get the user and movie counts.
# add unique index for users
u_uniq = ratings.userId.unique()
user2idx = {o:i for i,o in enumerate(u_uniq)} # object:index
ratings.userId = ratings.userId.apply(lambda x: user2idx[x]) # returns the index
# add unique index for ratings
m_uniq = ratings.movieId.unique()
movie2idx = {o:i for i,o in enumerate(m_uniq)}
ratings.movieId = ratings.movieId.apply(lambda x: movie2idx[x]) # returns the index
# count of users and movies
n_users=int(ratings.userId.nunique())
n_movies=int(ratings.movieId.nunique())
Training and Performance
To evaluate the model performance, we first define hyperparameters, such as embedding size, which is the “latent factors,” where we set K = 50. The validation indexes are a random sample of the training data, 20% by default. After creating the dependent and independent variables, we use the Fastai ColumnarModelData class as our data loader. The ColumnarDataModel class can handle continuous and categorical variables. It reads data from the data frame and iterates over batches and epochs in the training process.
We call the Fastai Fit() method, which takes as arguments the model, data loader class, and loss function. The Fastai Fit() method is capable of applying numerous optimization methods. Here we use the SGD (stochastic gradient descent) method with weight decay. In effect, the training stage finds the latent factors or weights of the User and Item matrices that minimize the loss function, MSE (mean-square error), and also tune the weights of our neural network.
The results below show an RMSE of 1.2 (square root of 1.43) for the matrix factorization model, K = 50, and Movie Lens dataset. This result is a significantly larger RMSE loss than the best in class results of 0.91 in [Librec] (https://www.librec.net/release/v1.3/example.html).
val_idxs = get_cv_idxs(len(ratings)) # default 20% of dataset
wd=2e-4 # weight decay
n_factors = 50 # dimensionality of embeddings matrix
x = ratings.drop(['rating', 'timestamp'],axis=1)
y = ratings['rating'].astype(np.float32)
data = ColumnarModelData.from_data_frame(path, val_idxs, x, y, ['userId', 'movieId'], 64)
model = MFCF(n_users,n_movies).cuda()
opt = optim.SGD(model.parameters(), 1e-1, weight_decay=wd, momentum=0.9)
fit(model, data, 10, opt, F.mse_loss)
epoch trn_loss val_loss
0 1.794021 1.800683
1 1.318704 1.505234
2 1.171994 1.446952
3 1.113008 1.444233
4 1.022484 1.434512
Deep Learning Collaborative Filter (DLCF)
The DLCF model (illustrated below) resembles the Matrix Factorization CF model described above but is more general because it accepts additional inputs, and performs more than simple matrix multiplication. It also has multiple hidden layers. The first layer of the deep-learning model is a set of embedding matrices for the user and item latent factors (the same as before), and other inputs, in this case, the “day” variable. In general, yet additional input variables, such as demographic information, season, holidays, could be added. The hidden layers are fully connected RELU cells, and the output layer is a single Sigmoid cell. As illustrated, the model in the figure is the most general of the three, which we consider.
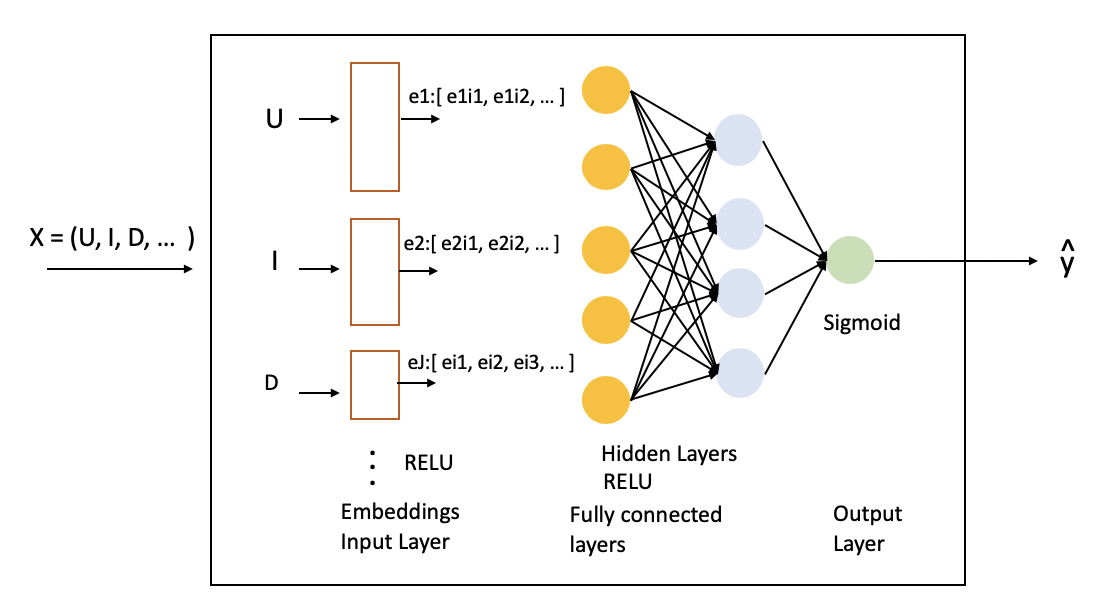
Henceforth, we evaluate the performance of three deep learning models, whose configurations are summarized in the table below, each with progressive capabilities. First, we gain an appreciation for a basic deep-learning latent factor model (DLCF1) without additional inputs; that is, it has the same inputs as the matrix factorization model. Then we add the day of the week as an input to the model (DLCF2). Finally, we add additional layers and cells per layer (DLCF3).
| Model | Description |
| DLCF1 | • K1 = 50 user factors, and K2 = 50 item factors. • 1 Hidden layer with NH = 10, RELU cells • 1 Sigmoid output cell |
| DLCF2 | • Similar to DLCF1 • Includes day of the week input, D, with KD = 3 |
| DLCF3 | • Similar to DLCF2 • Includes two hidden layers, and more cells per layer, NH = [50,30] |
DLCF Model 1 (DLCF1)
The code for our DLCF1 model is listed below. It contains input embeddings and one hidden layer. The constructor receives input parameters for initializing the embeddings matrices. For example, n_users corresponds to the number of users (rows), and n_factors is “K” the width of the user and item embeddings matrices. The dropout regularization percentages for the embeddings layer (p1) and hidden layer (p2) are also input.
def get_emb(ni,nf):
e = nn.Embedding(ni, nf)
e.weight.data.uniform_(-0.01,0.01)
return e
class DLCF1(nn.Module):
def __init__(self, n_users, n_movies, nh=10, p1=0.05, p2=0.5,):
super().__init__()
(self.u, self.m) = [get_emb(*o) for o in [
(n_users, n_factors), (n_movies, n_factors)]]
self.lin1 = nn.Linear(n_factors*2, nh)
self.lin2 = nn.Linear(nh, 1)
self.drop1 = nn.Dropout(p1)
self.drop2 = nn.Dropout(p2)
def forward(self, cats, conts):
users,movies = cats[:,0],cats[:,1]
x = self.drop1(torch.cat([self.u(users),self.m(movies)], dim=1))
x = self.drop2(F.relu(self.lin1(x)))
return F.sigmoid(self.lin2(x)) * (max_rating-min_rating+1) + min_rating-0.5
# this is genuine NN, though not very deep, 1 hidden layer
Several additional hyperparameters are defined next, including validation indexes, and weight decay.
val_idxs = get_cv_idxs(len(ratings)) # default 20% of dataset, see get_cv_idx in dataset.py
wd=2e-4 # weight decay, will talk about later, L2 regularization
n_factors = 50 # how big is embedding matrix, dimensionality of embeddings matrix
Next, we extract the minimum and maximum ratings for scaling the output. We specify Adam optimization with weight decay, specify the model, and call Fit().
min_rating,max_rating = ratings.rating.min(),ratings.rating.max()
wd=1e-5
model = DLCF(n_users, n_movies).cuda()
opt = optim.Adam(model.parameters(), 1e-2, weight_decay=wd)
fit(model, data, 5, opt, F.mse_loss)
epoch trn_loss val_loss
0 0.850864 0.803234
1 0.81824 0.793927
2 0.833568 0.786462
3 0.781164 0.783997
4 0.742855 0.781403
After 5 Epochs, the results are improved relative to the basic MFCF model. Though Adam optimization with weight decay improves the learning rate and helps to avoid local minima, the primary factor of improvement is bias terms for each cell in the neural network. The bias adjusts, for example, movies that universally get good or bad ratings or people who give consistently good or bad ratings. The RMSE is 0.883 (square root of 0.78), which is now meeting best in class results as compared to the [Librec] (https://www.librec.net/release/v1.3/example.html) benchmarks.
DLCF Model 2, day input (DLCF2)
We now enhance the DLCF model so that it can take in the additional categorical variable day and so that we specify an arbitrary number of hidden layers (see code listing below).
The model implements the more general deep-learning model, as illustrated above, and defaults to one hidden layer. As before, the constructor receives input parameters for initializing the embeddings matrices. For example, n_users corresponds to the number of users (rows) and nfu the width (K) of the user embeddings matrix. The first hidden layer will thus contain (nfu + nfd + nfd) cells. The dropout regularization percentages (embeddings layer and hidden layer(s)) are also input. The forward method forward propagates the inputs from the embeddings, fully connected layers, to the output.
def get_emb(ni,nf):
e = nn.Embedding(ni, nf)
e.weight.data.uniform_(-0.01,0.01)
return e
class DLCF2(nn.Module):
def __init__(self, n_users, n_movies, n_days, nfu, nfm, nfd,
nh = [10], drops = [.1, .5]):
super().__init__()
# create embeddings
(self.u, self.m, self.d) = [get_emb(*o) for o in [
(n_users, nfu), (n_movies, nfm), (n_days, nfd)]]
# default to 1 hidden layer
self.lin1 = nn.Linear(nfu + nfm + nfd, nh[0])
self.emb_drop = nn.Dropout(drops[0])
self.lins = nn.ModuleList([
nn.Linear(nh[i], nh[i+1]) for i in range(len(nh)-1)])
for drop in drops:
self.drops = nn.ModuleList([nn.Dropout(drop) for drop in drops])
self.lastdrop=nn.Dropout(drops[len(drops)-1])
self.lastlin=nn.Linear(nh[len(nh)-1],1)
def forward(self, cats, conts):
users,movies,days = cats[:,0],cats[:,1],cats[:,2]
x = self.emb_drop(torch.cat([self.u(users),self.m(movies),self.d(days)], dim=1))
x = F.relu(self.lin1(x))
for l,d, in zip(self.lins, self.drops):
x = d(x)
x = l(x)
x = F.relu(x)
x=self.lastdrop(x)
x=self.lastlin(x)
return F.sigmoid(x) * (max_rating-min_rating+1) + min_rating-0.5
Now we set up to train the DLCF2 model. Before training, we investigate the day variable. For example, perhaps a user prefers comedies during the week and action on Friday and Saturday. We begin by extracting the day of the week corresponding to the rating from the data set. The percentage of movies watched each day is illustrated below. From the plot below, we see that the most popular days for watching movies are Saturday, and Sunday with a notably smaller fraction of movies watched on weekdays.
from datetime import datetime
ep_to_day_lambda = lambda x:datetime.fromtimestamp(x/1000).strftime("%A")
ratings['day']=ratings['timestamp'].apply(ep_to_day_lambda)
ratings[['userId', 'movieId', 'rating', 'day', 'timestamp']].head()
ratings['day'].value_counts()/len(ratings)
Sunday 0.239151
Saturday 0.222996
Wednesday 0.140763
Monday 0.131947
Tuesday 0.108791
Thursday 0.082352
Friday 0.074001
Name: day, dtype: float64

For achieving the best performance results, the training and validation set should reflect the corresponding day percentages. Therefore, we define the stratified set of validation indexes below, which are input to the data loader.
from sklearn.model_selection import StratifiedShuffleSplit
category='day'
split = StratifiedShuffleSplit(n_splits = 1, test_size = 0.8, random_state = 42)
for val_idxs, _ in split.split(ratings, ratings[category]):
df_val = ratings.iloc[val_idxs].copy()
print(len(val_idxs))
val_idxs
As before, we specify the variables, but instead of one n_factors parameter (i.e., embeddings matrix width) parameter, we have several. Below we set the user and item factors to be the same as for DLCF1 above (embeddings width of 50). For the day input variable, the embeddings width is set to KD = 4. Again we employ Adam optimization with weight decay and call fit(). We achieve a small improvement from before, though the loss increases slightly on the final training epoch.
min_rating,max_rating = ratings.rating.min(),ratings.rating.max()
min_rating,max_rating
nfu = 50 # dimensionality of embeddings matrix
nfm = 50
nfd = 4
wd=2e-4
model = DLCF2(n_users, n_movies,n_days,nfu,nfm,nfd, nh=[30],
drops = [0.05, 0.5]).cuda()
opt = optim.Adam(model.parameters(), 1e-3, weight_decay=wd)
fit(model, data, 5, opt, F.mse_loss)
epoch trn_loss val_loss
0 0.77158 0.771764
1 0.763405 0.750387
2 0.73818 0.747482
3 0.749548 0.741922
4 0.735191 0.748893
DLCF Model 3, more layers (DLCF3)
This case is similar to the previous one. We do not change any of the inputs to the network. However, we modify the network to include an additional hidden layer, and each of the layers is larger, with 50 cells and 30 cells for the first and second hidden layers.
model = DLCF2(n_users, n_movies,n_days,nfu,nfm,nfd, nh=[50, 30],
drops = [ .05, .2, .5]).cuda()
opt = optim.Adam(model.parameters(), 1e-3, weight_decay=wd)
The larger network, DLCF3, achieves a slight improvement over DLCF2. The larger network seems to bring a little more stability.
fit(model, data, 5, opt, F.mse_loss)
epoch trn_loss val_loss
0 0.794924 0.76525
1 0.786284 0.746976
2 0.74575 0.735508
3 0.720929 0.736082
4 0.70611 0.735818
Summary: Collaborative Filtering with Deep Learning and Machine Learning
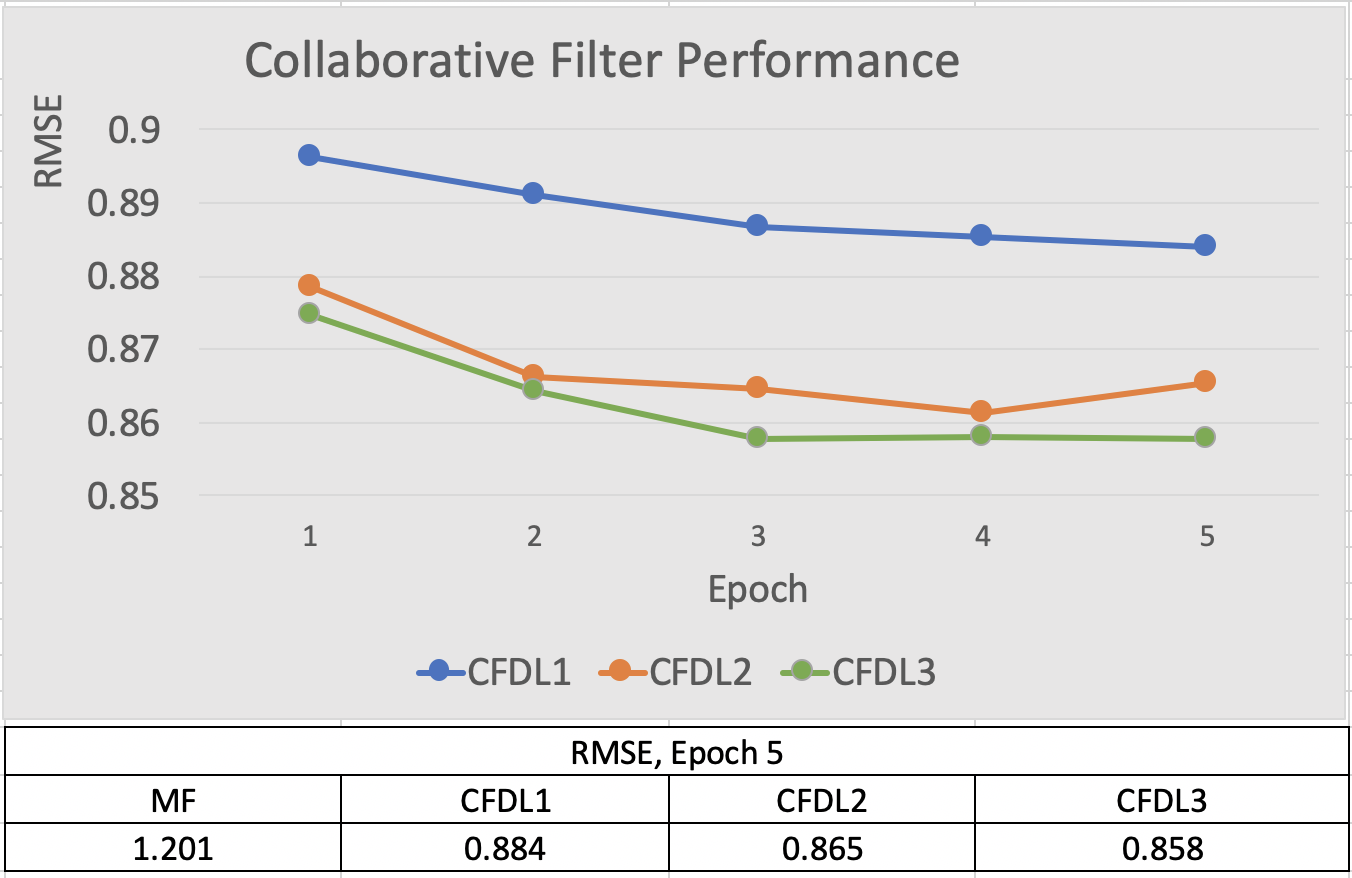
In summary, we evaluated four collaborative filter models, a conventional machine learning model (matrix factorization) and three deep-learning models. For convenience, the table below lists the salient attributes of each CF model and the critical performance differentiators. Additionally, the RMSE loss for the models is illustrated in the figure below, and the corresponding RMSE listed in the accompanying table
The deep learning collaborative filter models (DLCF 1,2, and 3) significantly outperform the MFCF model due to several factors, and each DLCF model offers progressive improvement. The DLCF1 model achieves a significant reduction of RMSE loss (36%) with an RMSE of 0.884 compared to the MFCF model with RMSE of 1.2. The factor attributed to this improvement is the bias terms for each NN cell, which compensate for user and movie bias. The additional input, “day” for the DLCF2 model, provides a modest improvement over DLCF1. The improvement from including the day is dependent on the data set, wherein larger or different datasets can potentially provide more improvement. The point here is to demonstrate how such additional inputs are combined with movie reviews. By adding these predictive inputs, the collaborative filter becomes a hybrid model, Collaborative Filter + Predictive Model. Similarly, DLCF3 offers minor performance gain; however, its convergence is a bit more stable versus DLCF2. DLCF3 includes two hidden layers versus one hidden layer in DLCF2. The key point for DLCF3 is to illustrate how to add hidden layers and nodes within a deep-learning collaborative filter architecture. This flexibility is useful when even more input types are input to the collaborative filter. Finally, the deep-learning models also include improved convergence capabilities that help to avoid local optima and speed up convergence. These include Adam optimization, weight decay, and dropout regularization.
| CF Model | Description | Differentiators |
| MFCF | Matrix factorization, latent factors, K = 50 (embeddings width), and SGD optimization | Solves for approximate ratings matrix based on minizing the MSE loss function with SGD |
| CFDL1 | One hidden layer, Latent factors K = 50 (embeddings width) NH = 10 (hidden units) with RELU activations, 1 Sigmoid output cell | Key performance differentiator (MSE) relative to MFCF model are the bias terms for each NN cell. Adam optimization with weight decay primarly provide improved learning rates relative to SGD |
| CFDL2 | Similar to CFDL1 + "Day" input | The additional input parameter (day) results in a small MSE performance improvement relative to CFDL1 |
| CFDL3 | Similar to DL3, plus multiple hidden layers (HL=2), and number of cells per hidden layer (NH = [50,30]) | The additional hidden layer and cells per hidden layer result in a slight improvement to performance, and stability. |
By evaluating and comparing a conventional matrix factorization model to deep-learning collaborative filter models, we’ve gained an appreciation for the differentiating characteristics of the models. To not lose sight of the bigger picture benefits, we also summarized the business applications where these models apply. The use of the PyTorch and Fastai libraries are employed to facillitate the code evaluations. A detailed Jupyter notebook is available (see the link above) with the full code listing for each example presented here. The results demonstrate how constructs such as embeddings, bias, and optimization functions work together to provide a superior RMSE loss performance as compared to the matrix factorization method. We also demonstrated how to enhance the deep-learning collaborative filter models with additional inputs to create a hybrid Collaborative Filter + Predctive Model and to scale them with additional hidden layers and nodes per hidden layer.